Matlab learning
作为一个计算机科班出身的人,很遗憾有太多知识没有及时学习,无论是哪种停滞不前的理由,此刻我们要相信,种树最好的时机是:十年前和现在。
接下来就开始小白学matlab啦!!!
之前看过几个视频教程,觉得matlab简直不要太强了,可以应用到很多方面,数学、计算机、控制等。在网上找到一个比较好的练习教程,主要作为学习的例子,链接如下:https://www.cnblogs.com/tiandsp/p/14337176.html
基础与技巧
优化拟合
1.高斯回归过程
看着教程了解点的高斯回归过程

- 高斯核函数背后的思想:简单与复杂的辩证,从线性模型到非线性模型。线性模型很棒,因为它们易于理解且易于优化。神经网络可以学习更复杂的决策边界,但会丢失许多线性模型的漂亮凸性。。是线性模型表现为非线性的一种方法是转换输入,例如:通过添加特征对作为附加输入,在这样的表示上学习线性模型是凸的。
不明确地扩展特征空间,是否可以在保留原始数据的同时,隐藏地处理特征扩张?这就是核方法
通过核方法,可以很好的处理线性不可分问题。简单性的哲学思想实质上就是,我们坚持寻找线性可分的转换问题,即变换数据,让它们线性可分,而变换数据的方法就是由低维到多维特征的一个特征空间变换。
高斯核函数可以把低维空间转化为无限维空间,同时又在实现了在低维计算高维点积。
第一、把有限空间映射到无限空间
核方法就是将数据空间放进更高维向量空间的方式,使得数据空间与高维空间中超平面的交点决定了数据空间中更复杂、弯曲的决策边界。
由(x,y)二维数据空间转换为五维空间
$$
(x,y,x^2,y^2,x^y)
$$
为了增加难度,甚至更高维的九维空间。九维空间
$$
(x,y,x^2,y^2,x^y,x^3,x^2y,xy^2,y^3)
$$
第二、从无限返回有限
在现实中,我们更需要用有限形式的计算表示无限维度的计算,避免维度灾难。
我们将通过每个点发送到无限向量来定义无限多项式核
$$
(x,y,x^2,y^2,x^y,x^3,x^2y,xy^2,y^3,x^4,……)
$$
实际上,原始的五维空间包含在这个无限维空间中。原始的五维核是我们通过将无穷多项式核投影到这个五维空间中得到的。
将原始数据空间中的核定义到无限维空间中,最常见的选择是高斯函数。将每个数据点发送到以某点为核的高斯函数。将原始数据空间中的每个点放入到更高(实际上是无限)的维向量空间。
在应用计算机处理时,将通过选择数据空间中的点(有限)来选择有限维空间,然后采用以这些点为中心的高斯斑点所跨越的向量空间。如在上文中,由无限多项式核的前五个坐标定义的向量空间。
投影:实现无限维空间返回到有限维
对于有限维向量,定义投影的最常用方法是使用点积:这是我们通过将两个向量的相应坐标相乘,然后将它们全部加在一起得到的数字。例如,三维向量的点积(1,2,3)和(2,5,4)的1·2+2·5+3·4=15,如果我们将两个高斯函数相乘并积分,则该数字等于中心点之间距离的高斯函数。
换句话说,高斯核将无限维空间中的点积转换为数据空间中点之间距离的高斯函数。
从有限维到无限维空间的思想,帮助我们更好的理解高维空间的线性可分思想;而从无限维返回到有限维,又让我们更好的理解其几何意义、更好的实现计算。
- 指数衰减函数:揭秘分类的精妙。
具有高斯核的SVM分类器简单地是在数据点和每个支持向量之间计算的核函数的加权线性组合。支持向量在数据点分类中的作用通过α(支持向量的全局预测有用性)和K(x,y)(支持向量在特定数据点的预测中的局部影响)来调和的。
下面开始matlab的代码学习。
1 | x=0:0.1:8; %原始数据 |
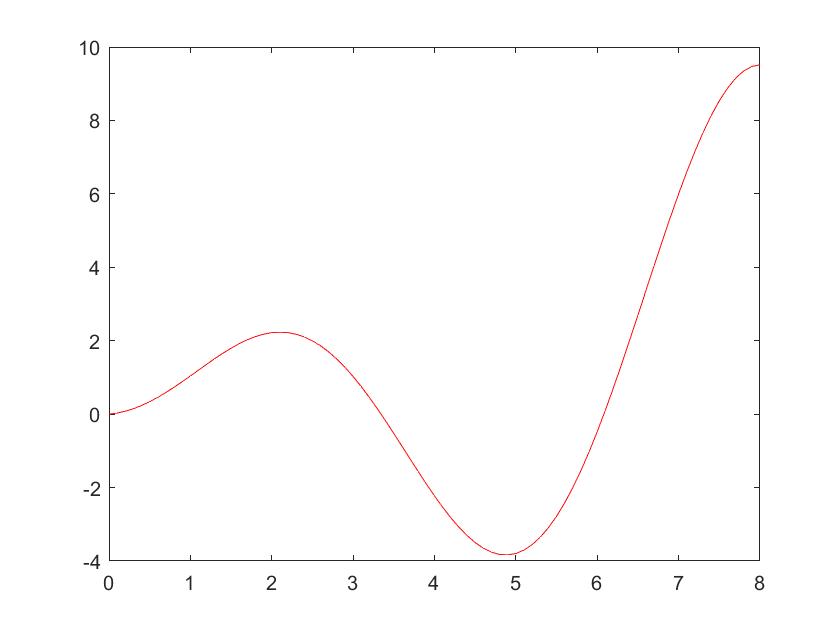
1 | gc_x = x(1:end); %观测数据加噪声 |
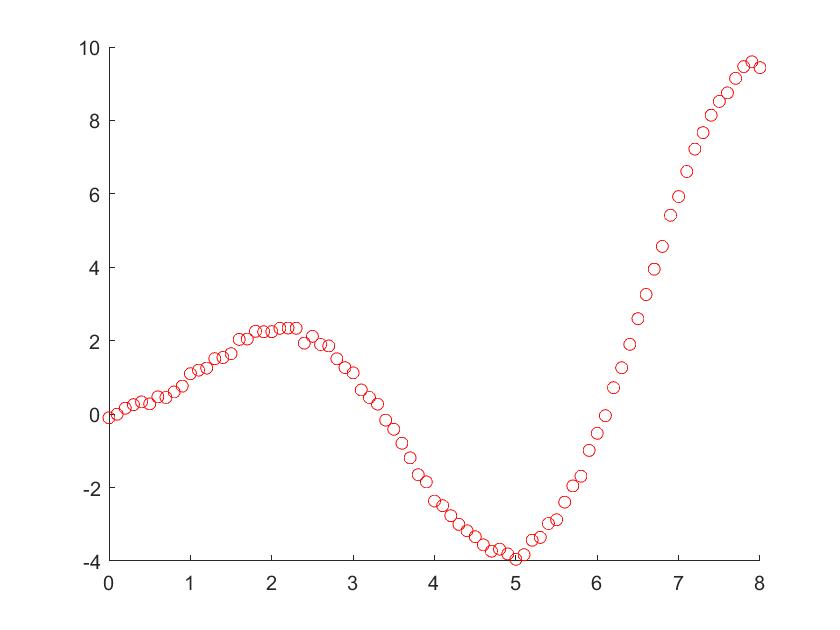
1 | x=0:0.1:8; %原始数据 |
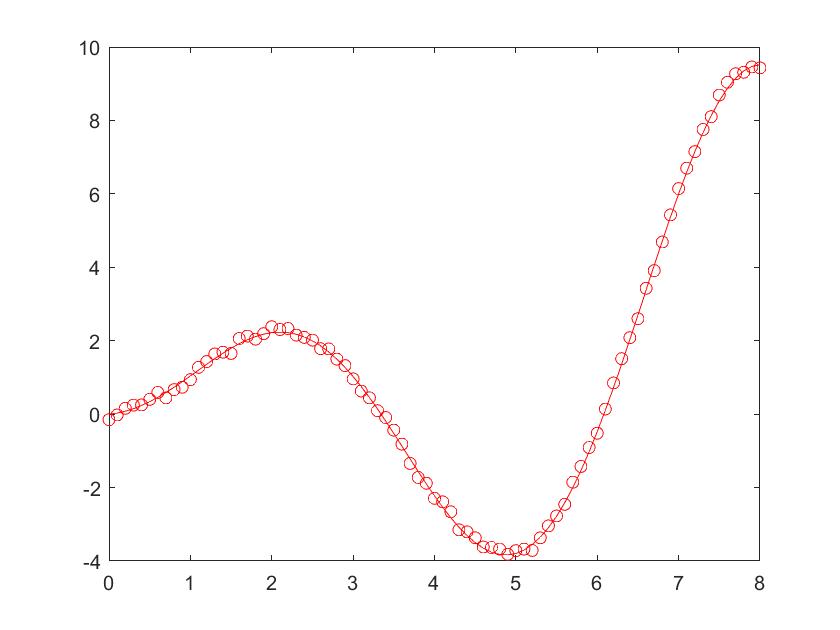
1 | sigma = 0.001; %sigma改成2可以明显看出方差范围 |
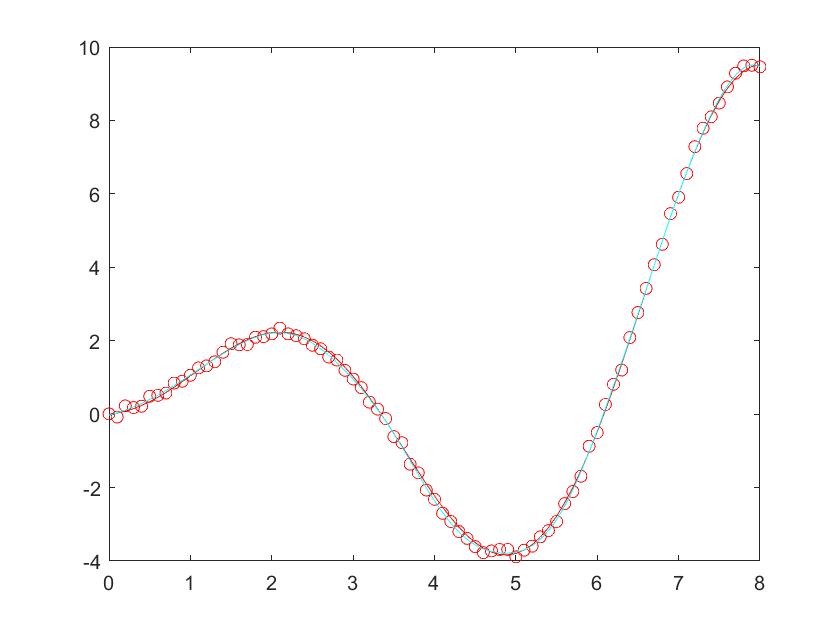
1 | %画出方差范围 |
1 | plot(x,max_y,'c'); |
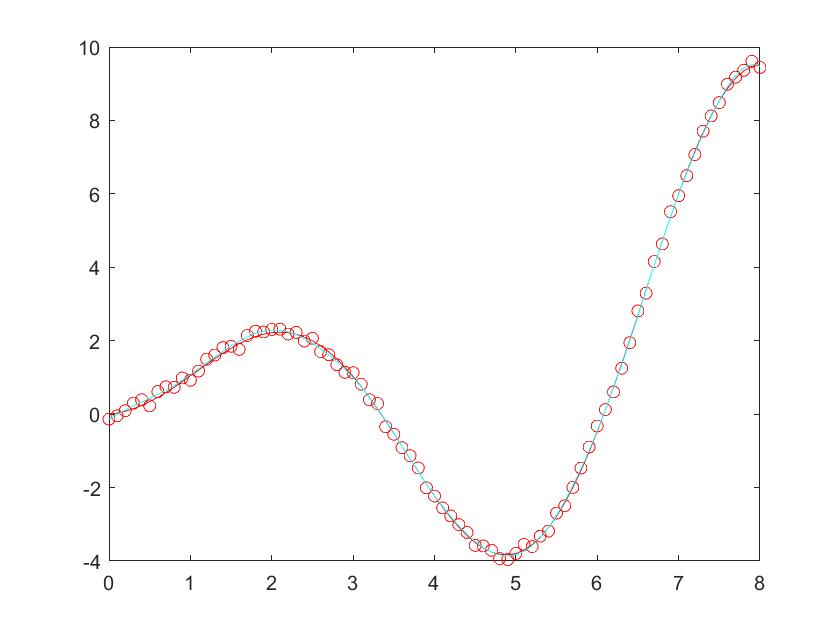
感觉这个对于基础学习似乎也不错:https://blog.csdn.net/qq_38431572/category_9417566.html
2 BFGS
感觉这个对于基础学习似乎也不错:https://blog.csdn.net/qq_38431572/category_9417566.html
1.拟牛顿法是求解非线性优化问题最有效的方法之一,DFP、BFGS方法以及L-BFGS算法都是重要的拟牛顿法
(1)原始牛顿法 :在现有极小点估计值的附近对f(x)做二阶泰勒展开,进而找到极小点的下一个估计值。
(2)阻尼牛顿法:由于原始牛顿法不能保证函数值稳定下降,提出了“阻尼牛顿法”,即寻找最优的步长因子。
2.拟牛顿法:不用二阶偏导数而构造出可以近似海森矩阵(或海森矩阵的逆)的正定对称阵,在“拟牛顿”的条件下优化目标函数,不同的构造方法就产生了不同的拟牛顿法。
拟牛顿条件或拟牛顿方程或割线条件:实质是对海森矩阵近似的理论依据。
3.DFPS
该算法的核心:通过迭代的方法,对
$$
H^{-1}{k+1}
$$
做近似。其迭代格式为
$$
D{K+1} = D_{K} + \vartriangle D_{K}
$$
4.与DFP算法类似,只是互换了其中的
$$
s_{k} 和 y_{k}
$$
整个算法不在需要求解线性代数方程组,由矩阵-向量运算就可以完成了。
5.L-BFGS
不在是用存储完整的矩阵,而是存储计算过程中的向量序列。
BFGS和DFP都是拟牛顿法,和高斯牛顿法不同的地方是不用直接求黑塞矩阵了,而BFGS又比DFP算法有更好的数值稳定性。
算法步骤如下:
\1. 给一个待求参数的初始值x(1)。
\2. 给定H(1)矩阵为单位阵,并且计算出待优化函数在x(k)处的梯度g(k)。
\3. 令d(k) = -H(k)*g(k),得到搜索方向。
\4. 从x(k)出发,沿着d(k)方向搜索,给定一个步长,找到其搜索范围内比当前参数x(k)更小函数值对应的x值,记为x(k+1)。
\5. 计算待优化函数在x(k+1)处的梯度g(k+1)。
\6. 计算此时参数位移p = x(k+1) - x(k)和梯度位移q = g(k+1) - g(k)。
\7. 最后根据下面迭代公式更新H矩阵即可,当g小于一定阈值时认为迭代结束。
下面两个公式是对偶的,形式上就是把p和q对换了一下,通常BFGS性能更优。
以下为一个NIST非线性拟合例题作为示例。
[https://blog.csdn.net/itplus/article/details/21897715]:
1 | data=[109 1; %待拟合数据 |
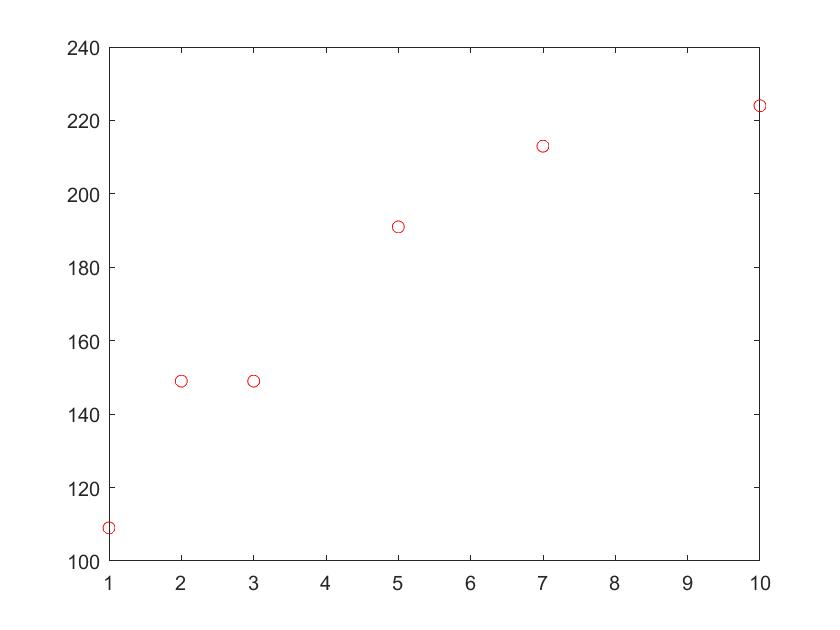
1 | syms b1 b2; |
1 | f=inline(char(ff),'b1','b2'); %转为函数 |
1 | b = [1;1]; %初始参数 |
1 | re=[]; |
1 | re=[]; |
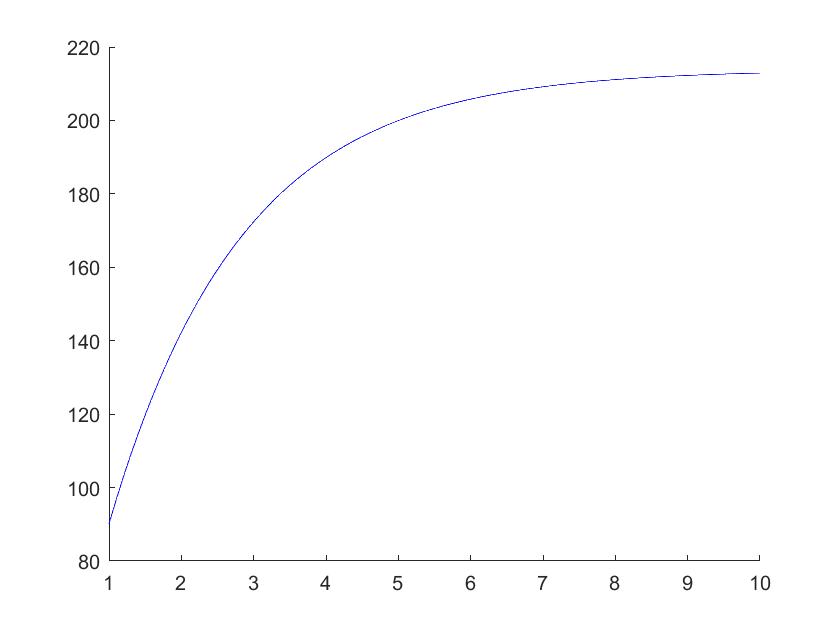
最终的结果图为